
Mathematica v7.0
分享到:
Mathematica是由沃尔夫勒姆研究公司研发的一款科学计算软件,很好的结合了数值和符号计算引擎、图形系统、编程语言、文本系统以及与其他应用程序的高级连接。从Mathematica刚被研发出来时,曾引起了科学、技术、媒体、等领域的轰动,被认为是一个革命性的进步。
Mathematica大多被工业和教育领域采用,并且许多机构将Mathematica当做标准工具来使用,其中包括美国政府的主要机构、全球最大的50所大学以及世界50强的所有公司。Mathematica的出现使得人们在科技和其他运用计算机的领域产生了深刻的影响。
使用Mathematica能够很好的帮助你完成许多数学方面的难题,虽然Mathematica多被科技工作者和其他专业人士使用,但是Mathematica却被广泛应用在教学中,大家都知道数学的许多计算非常复杂、繁琐,特别是一些函数还需要画出相应的函数图。大家都知道,不管是多有名的数学家都不能画出完美的函数图,但是借助Mathematica,用户能够轻松的解决许多数学难题。
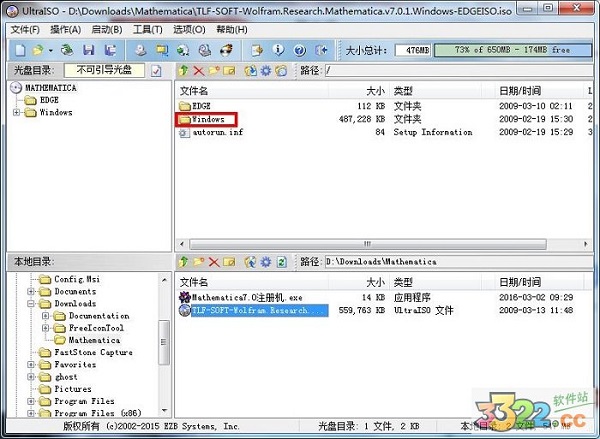
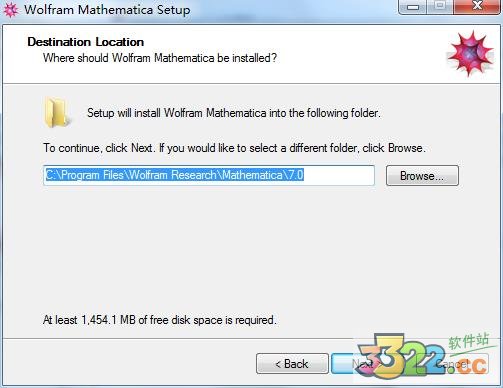
2、下一步后,选择安装路径,安装需要1.4G左右的空间,请用户选择空间比较打的磁盘安装,建议D、E、F盘。
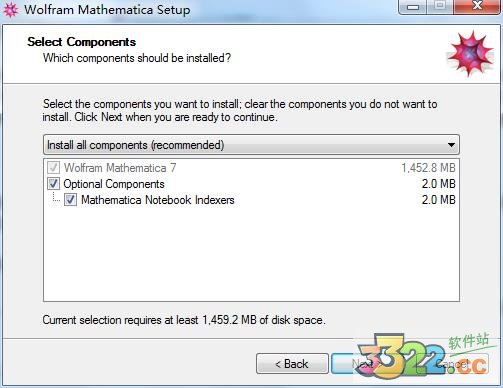
3、选择安装内容,默认就好。
4、一直点击下一步,等待安装完成。
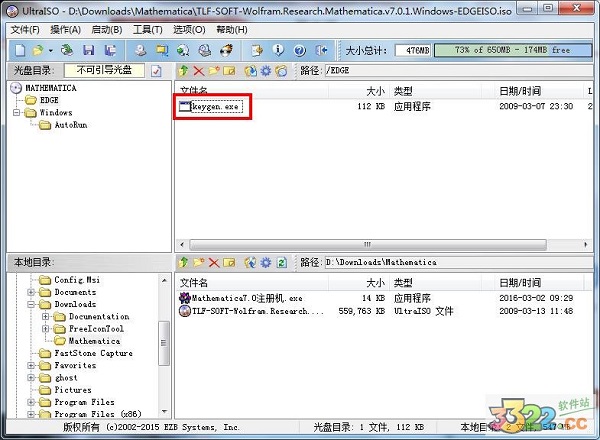
2、打开ISO文件中的EDGE文件夹中的注册机,将其中的License复制,输入到注册页面的框中。
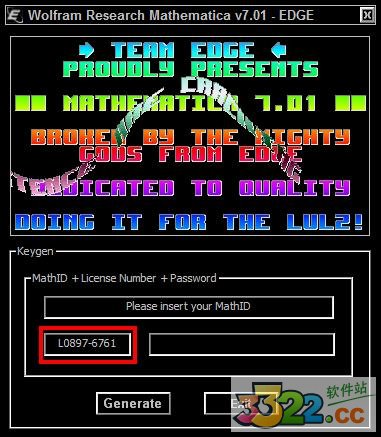
3、复制其中的math ID粘贴到注册机中。
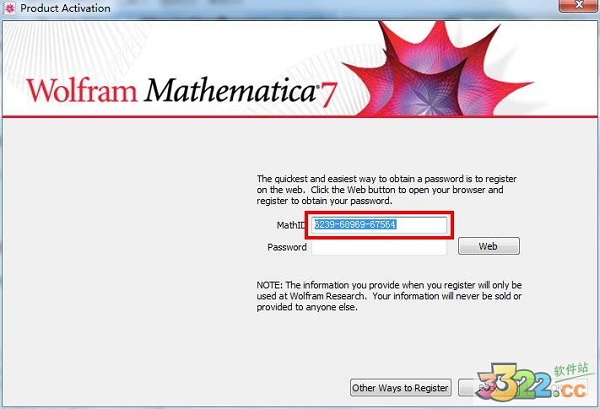
4、再将生成的密码输入到注册页面。
5、重启Mathematica,就能使用了
2、打开Mathematica,点击help中的Documentation Center。
引入了新一代的工业强度图像处理,内嵌入 Mathematica 的综合算法,编程和接口平台
2、内置的并行计算功能
利用最新的多核处理器与 Mathematica 的新的自动并行计算技术—完美地在您的机器上实现并行计算
3、图形自动制图
通过使用 Mathematica 的符号性架构,灵活的图形,以及自动计算美学,信息可视化算法向前迈出了巨大的一步。
4、矢量及场的可视化
创建自动优化的矢量场和流线可视化—可应用于液体、电力气学等领域。
5、完全支持样条曲线
充分融入计算和图形,在任何数量层面都具有世界上最通用的样条。
6、工业强度的布尔计算
把高性能的布尔分析、优化和验证运用到有着数以千计变量的系统中— 所有这些都已经整合入了Mathematica 的工作流程。
7、离散积分
成功实现运用全面的离散符号运算系统来解决新一代的离散问题。
8、时滞微分方程
时滞微分方程现在已成为Mathematica 的全自动数控微分方程求解的一个组成部分。
9、微分和差分根
Mathematica 7可直接处理微分和差分方程的隐式解 —由此极大地泛化了特殊函数的概念。
10、数论新功能
在分析、乘法数论和加法数论中,又有新的方面可被直接用于Mathematica 计算。
11、新类别的特殊函数
q函数,L-函数以及一系列其它函数,使Mathematica 拥有世界上最多的特殊函数。
12、强化的傅立叶分析
显式的傅立叶级数现在完全融入Mathematica 的符号功能。
2、自动计算美学
3、全自动图形布局
4、实时三维图形
5、自动表布局
6、动态互动
7、集成的几何计算
8、组合优化
9、约束非线性优化
10、等式定理证明
11、高级别字符串计算
12、新一代数值积分
现在,我对这一问题的认识是,所谓的软件的区别,恐怕也只是对我们入门用户而言的,如果真的熟练,只怕两个软件能做到的事的差别并不会有多大。我选择了mathematica,因为他的语句和传统数学式非常相近,符号计算的强大更是matlab所不具备的,至于数值计算,你有兴趣可以搜搜,截止目前我没有见过任何能说明mathematica的数值计算能力逊于matlab的证据,而且我个人恐怕是不会有什么要求高效率计算的程序需要运行的,所以mathematica对我来说足够了。另外,mathematica8有全中文自带帮助文档,十分适合自学,这也是我选择它的理由。
1.首先新建一个笔记本文件
2.最简单的一个例子,画出正弦函数的图像;利用Plot命令即可,函数可以自己修改
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}]
3.增加Frame命令可以使图像增加边框,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, Frame -> True]
4.增加GridLines命令可以使图像增加网格,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, GridLines -> Automatic]
5.增加PlotStyle命令可以改变图像线宽
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, PlotStyle -> {Thickness[0.01]}]
6.增加AxesLabel命令可以给坐标轴标记,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, AxesLabel -> {"x", "y"}]
7.增加Background命令修改背景颜色,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, Background -> RGBColor[0, 1, 0]]
2、Mathematica怎么求导?
D[Sin[[Beta][t]],t] 代码复制到软件里,shift+回车
3、Mathematica怎么输出jpg图片?
方法一
1.最简单的方法,但是不灵活。选择Figure文件的“File”菜单下面的“Save As...”。
2.在弹出的保存窗口中选择具体的保存格式,eps或jpg。另外该方法可以写成命令形式saveas(gcf,'1.eps')或saveas(gcf,'1.jpg'),方便在脚本文件中执行
方法二
该方法只能导出jpg格式的文件,供word中使用。具体方法是点击Figure窗口的“Edit”菜单,选择“Copy Figure”即可把图片导出到windows剪切板中。现在打开一个新的word文件,“Ctrl+v”即可把剪切板中的图片张贴到word中。
方法三
采用“Export”对话框进行导出,这也是我比较常用的。因为通常Figure图像边界有空白,上面两种方法需要手动设置figure坐标系的属性才能让图片布满整个窗口(当然也可以用脚本),比较麻烦。而本方法中的“Export”对话框能很好的解决。当然它还有其他更强大的功能。
4、mathematica怎么注释?
(*注释内容*)
就是两端加(*和*)作为注释的开头和末尾
5、mathematica pi怎么打?
a = {1}; s = N[{3*Sqrt[3]/2}, 18]; n = 31;
For[i = 2, i ≤ n, i++,
a = N[Append[a, Sqrt[2 - 2*Sqrt[1 - (a[[i - 1]]/2)^2]]], 18 ];
s = N[Append[s, 3*2^(i - 1)*a[[i]]], 18];
]
s1 = Table[s[[i + 1]] - s[[i]] , {i, 1, n - 1}];
Print["n", " s", "
", "s1"]
For[i = 1, i ≤ n - 1, i++,
Print[i, " ", s[[i]], " ", s1[[i]]]]
6、mathematica怎么解方程组?
用t表示θ,
方程为Solve[{a2 Cos[t1 + t2] + a1 Cos[t1] == x0, a2 Sin[t1 + t2] + a1 Sin[t1] == y0}, {t1, t2}]
解得:
{{t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(
2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(
2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(
2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}}
7、mathematica怎么画圆?
圆:Graphics[Circle[{0,0},半径],Axes->True]
椭圆:Graphics[Circle[{0,0},{半径1,半径2}],Axes->True]
双曲线、抛物线(通法)Plot[y/.Solve[一般式(=号用==),y],{绘图范围}]
8、mathematica怎么清屏?
方法1.当屏幕指令较多而影响查看时可以在命令窗口使用clear然后回车。
方法2.也可以点右键再点clear command window(清除命令窗口)。
方法3.使用clf,回车,清除上一幅图,在原图窗口再生成新图。
9、mathematica怎么输入矩阵?
输入矩阵:
用菜单里的Insert Table/Matrix
或者键盘输入Ctrl+,, Ctrl+Enter
输出矩阵就用MatrixForm就行了。
Mathematica大多被工业和教育领域采用,并且许多机构将Mathematica当做标准工具来使用,其中包括美国政府的主要机构、全球最大的50所大学以及世界50强的所有公司。Mathematica的出现使得人们在科技和其他运用计算机的领域产生了深刻的影响。
使用Mathematica能够很好的帮助你完成许多数学方面的难题,虽然Mathematica多被科技工作者和其他专业人士使用,但是Mathematica却被广泛应用在教学中,大家都知道数学的许多计算非常复杂、繁琐,特别是一些函数还需要画出相应的函数图。大家都知道,不管是多有名的数学家都不能画出完美的函数图,但是借助Mathematica,用户能够轻松的解决许多数学难题。

安装教程
1、解压缩后运行ISO文件中的“setup.exe”文件开始安装,注:Mathematica的安装程序必须使用虚拟光驱运行,请用户安装时注意,小编为你提供软碟通下载
2、下一步后,选择安装路径,安装需要1.4G左右的空间,请用户选择空间比较打的磁盘安装,建议D、E、F盘。

3、选择安装内容,默认就好。

4、一直点击下一步,等待安装完成。

破解教程
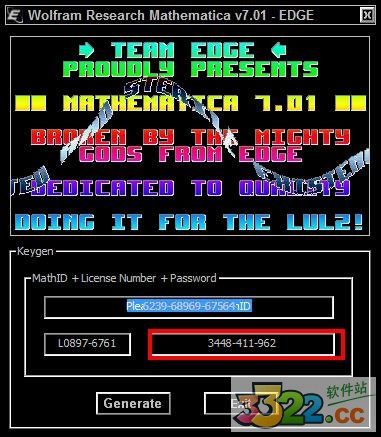
1、安装完毕如果直接点击Finnish的话,会自动打开程序。
2、打开ISO文件中的EDGE文件夹中的注册机,将其中的License复制,输入到注册页面的框中。

3、复制其中的math ID粘贴到注册机中。

4、再将生成的密码输入到注册页面。

5、重启Mathematica,就能使用了
汉化教程
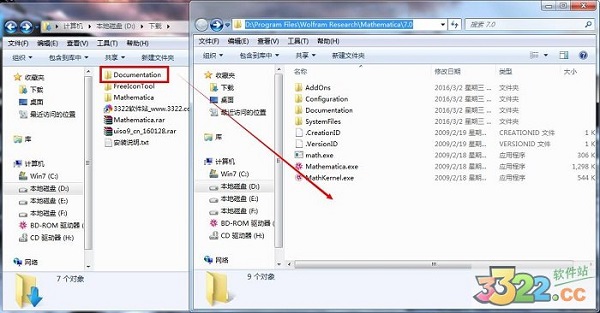
1、本软件的操作界面是英文的,但是小编将其中的帮助文档给汉化了,这样才能有好的使用Mathematica。将解压后的Documentation复制粘贴到安装目录下
2、打开Mathematica,点击help中的Documentation Center。
新功能
1、内置的数字图像处理与分析功能引入了新一代的工业强度图像处理,内嵌入 Mathematica 的综合算法,编程和接口平台
2、内置的并行计算功能
利用最新的多核处理器与 Mathematica 的新的自动并行计算技术—完美地在您的机器上实现并行计算
3、图形自动制图
通过使用 Mathematica 的符号性架构,灵活的图形,以及自动计算美学,信息可视化算法向前迈出了巨大的一步。
4、矢量及场的可视化
创建自动优化的矢量场和流线可视化—可应用于液体、电力气学等领域。
5、完全支持样条曲线
充分融入计算和图形,在任何数量层面都具有世界上最通用的样条。
6、工业强度的布尔计算
把高性能的布尔分析、优化和验证运用到有着数以千计变量的系统中— 所有这些都已经整合入了Mathematica 的工作流程。
7、离散积分
成功实现运用全面的离散符号运算系统来解决新一代的离散问题。
8、时滞微分方程
时滞微分方程现在已成为Mathematica 的全自动数控微分方程求解的一个组成部分。
9、微分和差分根
Mathematica 7可直接处理微分和差分方程的隐式解 —由此极大地泛化了特殊函数的概念。
10、数论新功能
在分析、乘法数论和加法数论中,又有新的方面可被直接用于Mathematica 计算。
11、新类别的特殊函数
q函数,L-函数以及一系列其它函数,使Mathematica 拥有世界上最多的特殊函数。
12、强化的傅立叶分析
显式的傅立叶级数现在完全融入Mathematica 的符号功能。
新特性
1、高影响力的自适应可视化2、自动计算美学
3、全自动图形布局
4、实时三维图形
5、自动表布局
6、动态互动
7、集成的几何计算
8、组合优化
9、约束非线性优化
10、等式定理证明
11、高级别字符串计算
12、新一代数值积分
和matlab功能对比
传统的说法是matlab擅长数值运算,尤其是矩阵数值运算,而mathematica擅长符号运算;此外matlab似乎是被国内的大家认识得更早,所以用的人疑似更多但是,就我个人暑假以来的使用经验来说,这些传统的说法不见得对。我在尝试解一个偏微分方程组的数值解,因此同时接触了这两个软件,并且也分别请教了一些会用这两个软件的人。现在的调查结果是,matlab的解偏微分功能很渣,号称有解相关问题的工具箱(对,工具箱,这是许多人力挺matlab的理由之一),只能解非常简单的偏微分方程,而据说功能更强的相关指令,要求手动把方程要化成标准形式——把偏微分方程化成标准形式谈何容易!?而mathematica,相关求解格式就要简单的多,虽然也经过了一些波折,但最后四处求助之后,好歹勉强把我所要解的问题给解出来了。现在,我对这一问题的认识是,所谓的软件的区别,恐怕也只是对我们入门用户而言的,如果真的熟练,只怕两个软件能做到的事的差别并不会有多大。我选择了mathematica,因为他的语句和传统数学式非常相近,符号计算的强大更是matlab所不具备的,至于数值计算,你有兴趣可以搜搜,截止目前我没有见过任何能说明mathematica的数值计算能力逊于matlab的证据,而且我个人恐怕是不会有什么要求高效率计算的程序需要运行的,所以mathematica对我来说足够了。另外,mathematica8有全中文自带帮助文档,十分适合自学,这也是我选择它的理由。
到底有多厉害?
在Programming Puzzles & Code Golf Stack Exchange上,有人发起了这么一个游戏(popularity contest - Showcase your language one vote at a time ):每个回答者选一种编程语言,先说一点关于这门语言的有趣事实;然后,如果获得N个赞,就可以添上长度从1到N不等的至多N条代码片段(中间可以跳过一些数字)来展示这门语言的各种特性。目前排在第一位的语言是Mathematica,获得了144个赞,恰好是第二名的两倍,比起Python、MATLAB之类的更是不知高到哪里去了。这个回答的作者是Martin Büttner。我就搬运一下,顺便翻译一下。原回答是按从长到短排列的,我把它倒了过来,还补上了若干作者已经删掉的代码片段。翻译得不好。欢迎去看原回答,有stackexchange帐号的话可以顺便点个赞。这个问题里其它语言的回答同样精彩。如何除后取余?
a={x} x=1,2,3,4,6…… 输出a{x}如何终止程序运行?
alt-.就是同时按下alt键和句号,注意标点状态应当是英文怎么用?
1、Mathematica怎么画图?1.首先新建一个笔记本文件
2.最简单的一个例子,画出正弦函数的图像;利用Plot命令即可,函数可以自己修改
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}]
3.增加Frame命令可以使图像增加边框,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, Frame -> True]
4.增加GridLines命令可以使图像增加网格,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, GridLines -> Automatic]
5.增加PlotStyle命令可以改变图像线宽
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, PlotStyle -> {Thickness[0.01]}]
6.增加AxesLabel命令可以给坐标轴标记,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, AxesLabel -> {"x", "y"}]
7.增加Background命令修改背景颜色,
Plot[Sin[(2*Pi)/3*t], {t, 0, 3}, Background -> RGBColor[0, 1, 0]]
2、Mathematica怎么求导?
D[Sin[[Beta][t]],t] 代码复制到软件里,shift+回车
3、Mathematica怎么输出jpg图片?
方法一
1.最简单的方法,但是不灵活。选择Figure文件的“File”菜单下面的“Save As...”。
2.在弹出的保存窗口中选择具体的保存格式,eps或jpg。另外该方法可以写成命令形式saveas(gcf,'1.eps')或saveas(gcf,'1.jpg'),方便在脚本文件中执行
方法二
该方法只能导出jpg格式的文件,供word中使用。具体方法是点击Figure窗口的“Edit”菜单,选择“Copy Figure”即可把图片导出到windows剪切板中。现在打开一个新的word文件,“Ctrl+v”即可把剪切板中的图片张贴到word中。
方法三
采用“Export”对话框进行导出,这也是我比较常用的。因为通常Figure图像边界有空白,上面两种方法需要手动设置figure坐标系的属性才能让图片布满整个窗口(当然也可以用脚本),比较麻烦。而本方法中的“Export”对话框能很好的解决。当然它还有其他更强大的功能。
4、mathematica怎么注释?
(*注释内容*)
就是两端加(*和*)作为注释的开头和末尾
5、mathematica pi怎么打?
a = {1}; s = N[{3*Sqrt[3]/2}, 18]; n = 31;
For[i = 2, i ≤ n, i++,
a = N[Append[a, Sqrt[2 - 2*Sqrt[1 - (a[[i - 1]]/2)^2]]], 18 ];
s = N[Append[s, 3*2^(i - 1)*a[[i]]], 18];
]
s1 = Table[s[[i + 1]] - s[[i]] , {i, 1, n - 1}];
Print["n", " s", "
", "s1"]
For[i = 1, i ≤ n - 1, i++,
Print[i, " ", s[[i]], " ", s1[[i]]]]
6、mathematica怎么解方程组?
用t表示θ,
方程为Solve[{a2 Cos[t1 + t2] + a1 Cos[t1] == x0, a2 Sin[t1 + t2] + a1 Sin[t1] == y0}, {t1, t2}]
解得:
{{t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(
2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(
2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 -> -ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(
2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 - [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> -ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}, {t2 ->
ArcCos[(-a1^2 - a2^2 + x0^2 + y0^2)/(2 a1 a2)],
t1 -> ArcCos[(a1^3 x0 - a1 a2^2 x0 + a1 x0^3 +
a1 x0 y0^2 + [Sqrt](-a1^6 y0^2 + 2 a1^4 a2^2 y0^2 -
a1^2 a2^4 y0^2 + 2 a1^4 x0^2 y0^2 + 2 a1^2 a2^2 x0^2 y0^2 -
a1^2 x0^4 y0^2 + 2 a1^4 y0^4 + 2 a1^2 a2^2 y0^4 -
2 a1^2 x0^2 y0^4 - a1^2 y0^6))/(2 (a1^2 x0^2 +
a1^2 y0^2))]}}
7、mathematica怎么画圆?
圆:Graphics[Circle[{0,0},半径],Axes->True]
椭圆:Graphics[Circle[{0,0},{半径1,半径2}],Axes->True]
双曲线、抛物线(通法)Plot[y/.Solve[一般式(=号用==),y],{绘图范围}]
8、mathematica怎么清屏?
方法1.当屏幕指令较多而影响查看时可以在命令窗口使用clear然后回车。
方法2.也可以点右键再点clear command window(清除命令窗口)。
方法3.使用clf,回车,清除上一幅图,在原图窗口再生成新图。
9、mathematica怎么输入矩阵?
输入矩阵:
用菜单里的Insert Table/Matrix
或者键盘输入Ctrl+,, Ctrl+Enter
输出矩阵就用MatrixForm就行了。
展开更多
Mathematica v7.0下载地址
- 需先下载高速下载器:
- 专用下载:
- 其它下载:







































