
信任的进化
分享到:
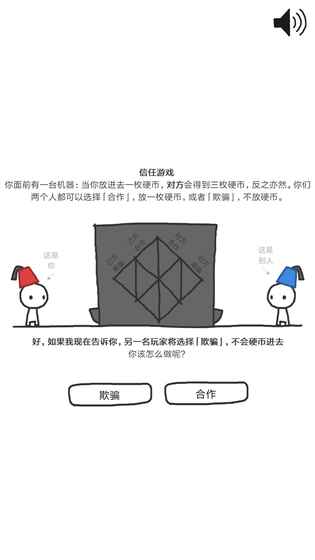
信任的进化这个游戏的原理来源于博弈论。许多年前,一个博弈论学家试图破解博弈论经典模型囚徒困境(这个游戏就是以重复的囚徒困境为基础,即合作双赢、一方欺骗得利、都欺骗则皆损),试图用不同的程序之间进行重复的计分博弈,并仿照生物物竞天择,分数高的程序得以繁衍,分数低的程序将被淘汰。他邀请了许多博弈论学家与数学家设计了数十个不同的程序,参与这个项目,设计的项目中不乏逻辑十分复杂的高端程序,但令人惊讶的是,最终获得最高分数的是源于一名数学家设计的逻辑极为简单的程序,被称为“以牙还牙”,其逻辑非常简单,就是重复对手上一步选择,这也就是游戏中被称为“复读机”的程序(现实中“以牙还牙”的人也是人们最不愿意惹的虽然“报仇”不会带来利益反而会损失利益,但会让人知道其后果而不敢惹你),而这次实验,也演变为游戏中的交互重复博弈。因此,这个博弈论史上经典的实验对于游戏的理解有很大的帮助。这次实验中,总分前十的程序有九个为善意程序,即总是优先考虑合作的程序。这是为什么呢?虽然在博弈繁衍初期恶意程序占尽便宜,但一旦繁衍起来,恶意程序相互欺骗,分数低迷,难逃淘汰。另一边,善意程序相互信任,相互合作,不断繁衍,最终繁衍生息,成为各种程序中的主体,但恶意程序并不用因此完全淘汰,因为一旦善意程序发展壮大,恶意程序又有了生存空间……那么总分前十为何还有一个不是善意程序呢?这个程序就是“谢灵顿程序”,它的逻辑是:一开始选择合作,发现对方总是合作就欺骗,在欺骗后发现对方马上报复后选择合作,重复以往,简而言之就是“欺软怕硬”。那为什么游戏轮数会设置4~7轮不固定呢?这设计到博弈论中蜈蚣博弈的问题,即倒退思维。假设你已经知道这是最后一轮博弈了,出于收益考虑你还会在最后一轮合作吗?最后一轮,无论对方做什么选择,出于收益欺骗是一定的选择。于是乎就确定了双方在最后一轮一定会欺骗。你知道对方在最后一轮一定会欺骗,那么何不在倒数第二轮讹对方一笔呢,因为最后一轮的选择没得选,那么倒数第三轮的就成了所谓的“最后一轮”,最后的欺骗将再次上演,接着推理到倒数第三轮也是如此……于是,从第一轮开始,大家都选择了欺骗(或许这就是“千年老油条”的逻辑),为何严格的推理反而造就了最低的收益?问题出在哪里?当然就是因为有确定的轮数,一旦没有确定的轮数,就没有确定的终点,也就没有所谓的蜈蚣博弈倒推。我们现实也不是如此?正因为不知道双方的合作关系什么时候会结束,店铺老板会热情的接待顾客,希望顾客再次购买;生意伙伴会保持来往,以期再次合作。但如此设置4~7随机轮次也并非万全之策,只能说不错,因为一旦与同一对手博弈了6轮若还有博弈,我依旧知道下一轮是最后一轮。

1、修复游戏Bug
2、对部分游戏功能进行全面优化



更新日志
信任的进化 V1.2.0更新内容1、修复游戏Bug
2、对部分游戏功能进行全面优化












































